Abwicklung des Rumpfes
Die Plattengänge für dieses Boot wurden mit partiellen Kegel- und Zylinderteilen angenähert/geformt. Im Folgenden eine kurze Darstellung der Vorgangsweise. Ausdrücklich werden hier nur die Schritte für dieses Boot skizziert. Für andere Bootsformen könnten sich andere Wege und Einstellungen ergeben. Vorausgesetzt wird Wissen um die Möglichkeiten, krumme Flächen mit abwickelbaren Flächen anzunähern. Man kann solche Abwicklungen natürlich auch auf Papier mit Bleistift und Lineal erreichen, wie es in vielen Publikationen für den Amateurbootsbau beschrieben wird bzw. verwendet eines der angebotenen Programmpakete. Da in den für uns erschwinglichen Sphären solcher Programme für die meiste Arbeit der Konstruktion eines Bootes letztendlich noch zusätzlich ein CAD-System gefordert wird, haben wir uns gleich für ein solches entschieden und den vorliegenden Versuch der semiautomatischen Abwicklung durchgeführt.
Mit dieser Version war ein komplettes 3D-Konstruieren möglich und auch das Erstellen von Makros war nicht schwierig. Für diese Aufgabe sollten folgenden Funktionen in einem CAD-System zur Verfügung stehen:
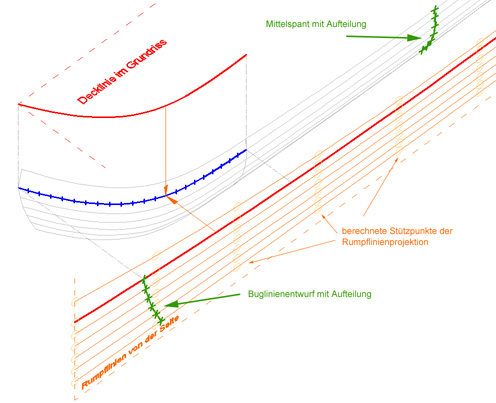
Für die folgenden Berechnungen wurde MS-Excel verwendet. Aus skizzierten Stützstellen von Rumpflinien in Grund- und Aufriss wurden 3 -5 Punkten übernommen, damit eine mathematische Funktion erstellt, um dann eine dichte Punktfolge zu rechnen. Die Übernahme ins Autocad erfolgte mit Copy-Paste (hier Dezimalzeichen "," durch "." ersetzt). Die weitere Konstruktion erfolgte dann dort. Die Übernahme von 3-5 Punkten und die Berechnung einer Funktion (Buglinie und Hecklinie im Grundriß als Funktion mit X**4, die Decklinie mit einer Funktion X**2, beide mit Ausgleichsrechnung erstellt) entspricht dem Straken mit einer Latte. Der Rumpf wurde in drei Abschnitten betrachtet. Der Bugabschnitt bis zum Übergang in den eher geraden Mittelteil und der Heckabschnitt, wieder stärker gekrümmt. Der Bug und das Heck sollte nach Kegeln, der Mittelteil nach Zylindern abgewickelt werden, der Boden aus Zylinder- und Kegelstücken. Begonnen wurde mit einer freien Skizze der Decklinie im Grundriß. Einige Punkte entlang dieser Linie gingen in einen Ausgleich für eine Funktion 4. Grades ein, erstellt in Excel, wo man auch eine schnelle Darstellung in einem Diagramm erreichen kann. Eine mittlere Anzahl von dann berechneten Stützpunkten wurde zur Kontrolle ins Autocad übernommen, mit einem Spline verbunden und auf Zufriedenheit über die Form geprüft. Nach einigen Korrekturläufen, wurden dann die Kurvenpunkte in einem regelmäßigen Abstand (hier ca. 20 cm) in Autocad automatisch gezeichnet (siehe Abbildung 1 : Grundriß der Decklinie) Desgleichen wurden die Decklinie in der Seitenansicht skizziert, anschließend mit einer Funktion 3. Grades ausgeglichen. (siehe Abbildung 1 : Seitenansicht der Decklinie). Damit war auch je ein Punkt als Schnittpunkte mit der skizzierten Buglinie, Mittelspant und Hecklinie definiert. Die weiteren Rumpflinienformen in der Seitenansicht ergaben sich durch eine Aufteilung der skizzierten Bug-, Heck und Mittelspantlinie um die gewünschte Anzahl der Plattengänge. Hierzu wurden die drei Punkte an der Bug-, Heck- und Mittelspantlinie in eine Funktion 3. Grades übernommen und weiter siehe oben.
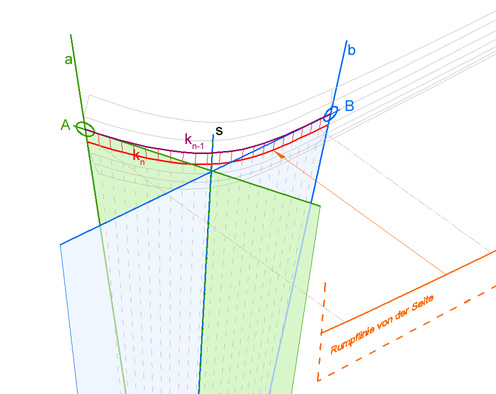
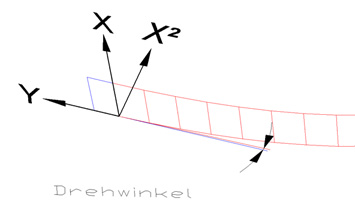
Abbildung 1 Von den regelmäßigen Stützstellen der definierten Buglinie im Grundriß wurden in Z-Richtung Strahlen gezogen und dann in der Seitenansicht an der Decklinie gekürzt. Hiermit ergab sich die Decklinie im Raum. Damit war die Decklinie rund um den Rumpf gegeben. Konstruiert wurde natürlich nur eine Hälfte des Rumpfes. Mit der Decklinie konnten nun die weiteren Rumpflinien im Raum wie folgt konstruiert werden. (siehe Abbildung 2, hier nur für den Bug ausgeführt). Im Prinzip war ein Kegel pro Plattengang zu konstruieren, wobei eine Tangentialebene am Bug und eine zweite am Übergang zum Mittelteil anliegt. Auf der Schnittgerade dieser beiden Ebenen muss die Spitze des Abwickelkegels liegen. Im Punkt A wurden zwei Strahlen gezeichnet. Einer läuft durch den 2. Punkt entlang der Decklinie (annähernd eine Tangente entlang der Decklinie im Bug) der zweite Strahl durch den nächsten Buglinienpunkt (annähernd eine Tangente an die Buglinie. Aus diesen beiden Strahlen wird eine Ebene definiert (grün), welche die Tangentialebene im Bug am ersten Plattengang (näherungsweise) darstellt. Im Punkt B wurde nach der gleichen Art eine Tangentialebene im Übergangsspant zum Mittelteil erreicht. Achtung, die Schnittpunkte der beiden Tangentenpaare sind nur scheinbare Schnittpunkte in der jeweiligen Ansicht. Die Schnittgerade der beiden erreichten Ebenen muss erst noch konstruiert werden. In Punkt A wird ein Koordinatensystem durch 3 Punkte definiert. Punkt A, Punkt auf der Tangente an die Buglinie und Punkt auf der Decklinientangente. Nach einer anschließenden Drehung um die Y-Achse und dem Wechseln in diese Ansicht, sieht man die definierenden Tangenten bzw. Ebene projizierend, d.h. als eine Linie. Und man sieht einen Schnittpunkt mit der Tangente an den Spant aus Punkt B. Hier setzt man einen Punkt auf diesen scheinbaren Schnittpunkt, allerdings auf die Tangente im Spant. In Autocad wird dies durch die Anzeigenreihenfolge für die Spanttangente erreicht, indem diese Linie ganz nach oben setzt. Dies ist ein Punkt auf der Schnittgerade der beiden Ebenen. So verfährt man auch beginnend in Punkt B. Eine zweiter Punkt der Schnittgerade wird konstruiert. Durch diese beiden Punkte läuft dann die Schnittgerade (s), auf welcher auch die Spitze des Kegels liegen muss. Die Spitze des Kegels kann eigentlich beliebig entlang von s festgelegt werden. Je weiter man diesen Punkt von dem zu erstellenden Plattengang weg legt, desto „senkrechter“ werden die Erzeugenden des Kegels die Rumpflinie schneiden. Dies kann für die Fertigung der Plattengänge von Vorteil sein, da ein Biegen einfacher sein dürften. Außerdem werden bei Spantenbauweise die eingebogenen Plattengänge näher an die Spanten zu liegen kommen. Hier wurde der Mittelpunkt zwischen den beiden gefundenen Schnittgeradenpunkten verwendet, dieser lag meist günstig. Für andere Bootsrümpfe könnte eine wesentlich andere Lage auf (s) sinnvoll sein, um z.B. den Übergang zum benachbarten Plattengang runder zu gestalten. Diese beiden Schnittpunkte können auch oberhalb eines Plattengangs zu liegen kommen, je nach Verlauf (siehe Schanzkleid, das hier nach innen fällt).
Abbildung 2
Nun zieht man Strahlen von der Kegelspitze (in der Abbildung unten, nicht dargestellt) zu den Stützpunkten der Rumpflinie (Kn-1). In der Seitenansicht werden nun diese Strahlen an der entsprechenden Rumpflinie im Seitenriß gekürzt und damit die Knicklinie kn entlang der abgeschnittenen Erzeugenden im Raum erreicht. Jeweils zwei benachbarte Strahlenabschnitte ergeben ein ebenes Viereck. In den Übergängen liegt oft der vierte Punkt außerhalb der Platte. Hier hilft man sich mit Dreiecken, die durch Abschneiden des überstehenden Vierecks am Gangende erreicht werden. (siehe Abbildung 3 im Bug) Kleine Flächen kann man auch noch zusammenfassen, sofern der Genauigkeitsverlust in Grenzen bleibt. Eventuell war der hier gewählte Stützpunktabstand entlang der Knicklinien für die reine Abwicklung zu dicht gewählt, für die Darstellung des Rumpfes als Bild aber von Vorteil und damit der Aufwand gerechtfertigt. Für vorbereitende Konstruktionsversionen wird eine weniger dichte Stützpunktfolge empfohlen. Die Vierecke und Dreiecke wurde mit 3D-Polygonen nachgezogen und in Regionen umgewandelt (Autocad-spezifisch ?, Regionen müssen eben sein). Gelingt dies, hat man die Sicherheit, dass tatsächlich alle beteiligten 3 oder 4 Punkte in einer Ebene liegen. Gleichzeitig kann man sich den fertigen Rumpf „shaded“ aus allen Richtungen betrachten, sozusagen als Belohnung (siehe Abbildung 3).
Abbildung 3 Die Bodenplatte kann man bei dieser Bootsform sehr einfach durch legen von parallen Strahlen (= Zylinder mit projizierter Knicklinie als Grundlinie) im gewünschten Winkel durch die Stützpunkte des ersten Knicks legen, mit der Mittelachse kürzen und dann wieder die Regionen über 3D-Polygone bilden. Im Heckbereich werden Strahlen von einem Übergangspunkt aus gelegt (= Kegel mitmit projizierter Knicklinie als Grundlinie). Die Regionen sind dann Dreiecke. Nun geht’s an die Abwicklung der Plattengänge. Dies ist ein sicherlich zeitraubender Vorgang, man kann es sich bis zur Endversion der Rumpfkonstruktion aufsparen, für den Zuschnitt des Baumaterials.
Abbildung 4
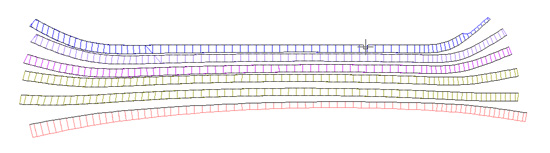
Die Abfolge von mehreren Drehungen und Funktionen kann man in einem Makro zusammenfassen. Das Ergebnis sind dann die Zuschnittspläne für die Plattengänge (Abbildung 5)
Die fertigen Linien übereinandergelegt ergeben das „Schnittmuster“, das mit einem Schnitträdchen aus Großmutter’s Nähkiste auf das Baumaterial oder wie hier, zuerst auf dünne HF-Platten übertragen wird. Diese Holzplatten können dann beim Bau nach dem Anpassen ev. noch leicht korrigiert werden. Anschließend werden die Aluplatten mit einem Plasmaschneider entlang dieser Platten ausgeschnitten.
Abschließend noch ein paar Bemerkungen zur Genauigkeit. Für die Abschätzung der Längengenauigkeit kann man einen Spline im Grundriß, etwa in der Form der Decklinie durch ein Polygon mit einzelnen Stützpunkten in gewünschter Dichte annähern. Man misst beiden Linienzüge und erhält dann eine Differenz bei gewählter Punktdichte. Damit lässt sich vorab der Aufwand (= Dichte der Stützpunkte) nach dieser Methode anpassen bzw. die erreichbare Genauigkeit beim Bau abschätzen. Für die Genauigkeit der Plattenbreiten wird eher die Übertragung der Schnittmuster (sind Polygonzüge) auf das Material ausschlaggebend sein, ein sinnvolles Straken der Linien wird eine ausreichende Genauigkeit bringen. Die Genauigkeit der einzelnen Stützpunkte selbst bleibt von der Punktdichte unberührt. Für die Übergänge entlang der Plattenteile wird die Genauigkeit des hier vorgestellten Verfahrens ausreichend sein. Man könnte die Tangentialebenen natürlich noch besser definieren. Liegen aber keine extreme Krümmungen in der Nachbarschaft von Übergängen, wird eher die CAD-Genauigkeit besser als die Realität beim Bau bleiben. Hier ist einfachere Beschreibung von einer Zylinder und Kegelabwicklung zu finden. Diese könnte auch allein mit Bleistift, Lineal und Papier bzw. mit enem einfachen Zeichenprogramm durchgeführt werden. |